i have a bunch of disconnected thoughts from the flip project lol
c++ -_-;
i have absolutely no idea how the source code for the original finds solutions or even like, represents the board? like, theres systems of equations and gaussian elimination and hex bitmaps and its all genuinely over my head. tho i do know what a 2-3-4 tree is now. i wanna do a visualization of one somehow
definitions
im gonna use some made up terminology to describe this game because i havent done enough research to know the actual terminology lol.
| boardstate | the set of states of all the squares, whether theyre black or white |
|---|---|
| stepstate | the set that the solver shows, the set of moves you'd have to make to achieve the current boardstate from a solved board or vice versa |
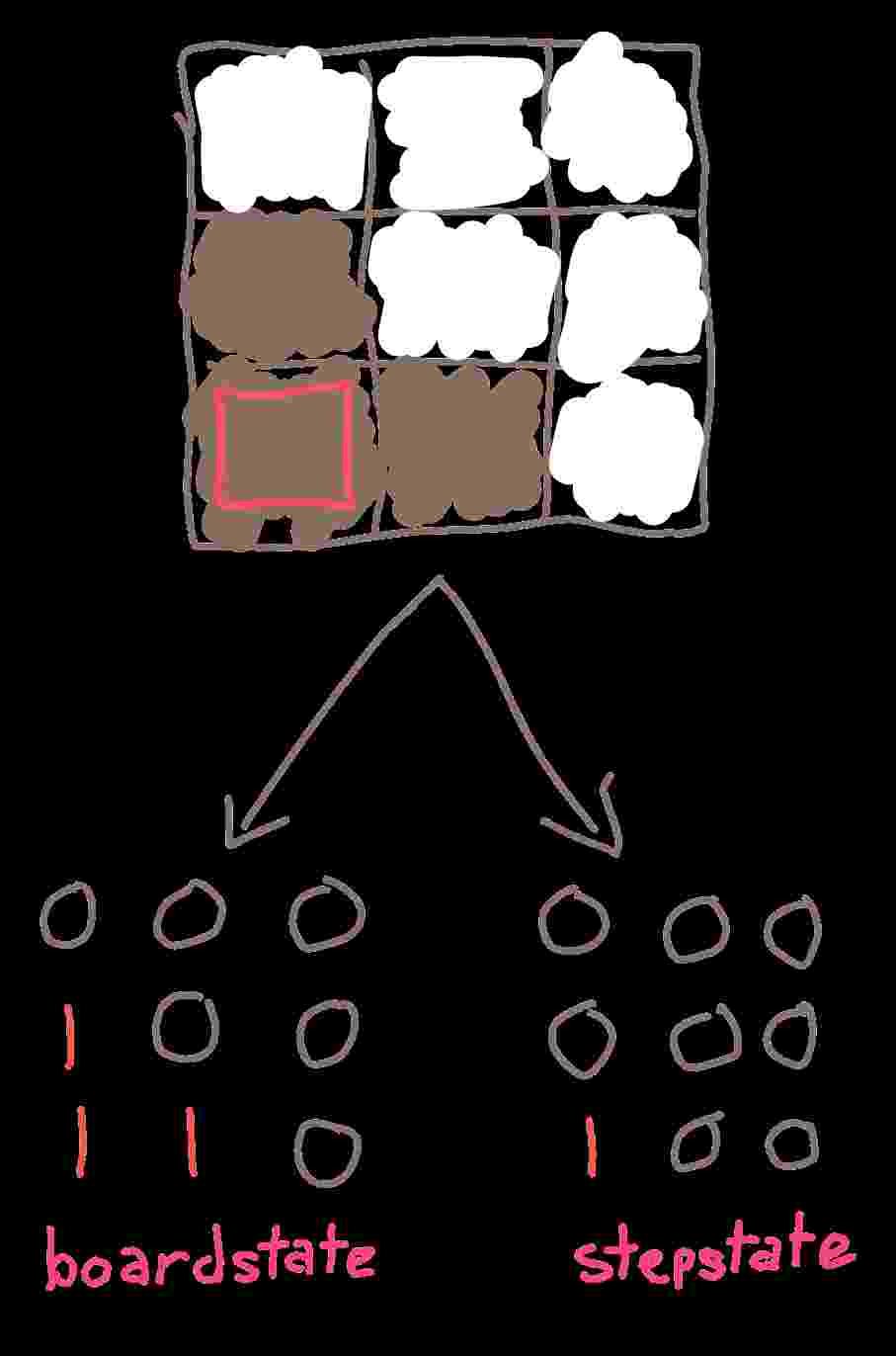
equivalency evenness
so the solver! the solver tries to check all solutions to a boardstate and pick the simplest one. it does this by precalculating a list of stepstates that produce a blank board (by iterating thru all possible stepstates). i reckon if u xor one of these equivalencies with the current stepstate, youll change the current stepstate but not the current boardstate. check out this example where every square is visited exactly twice
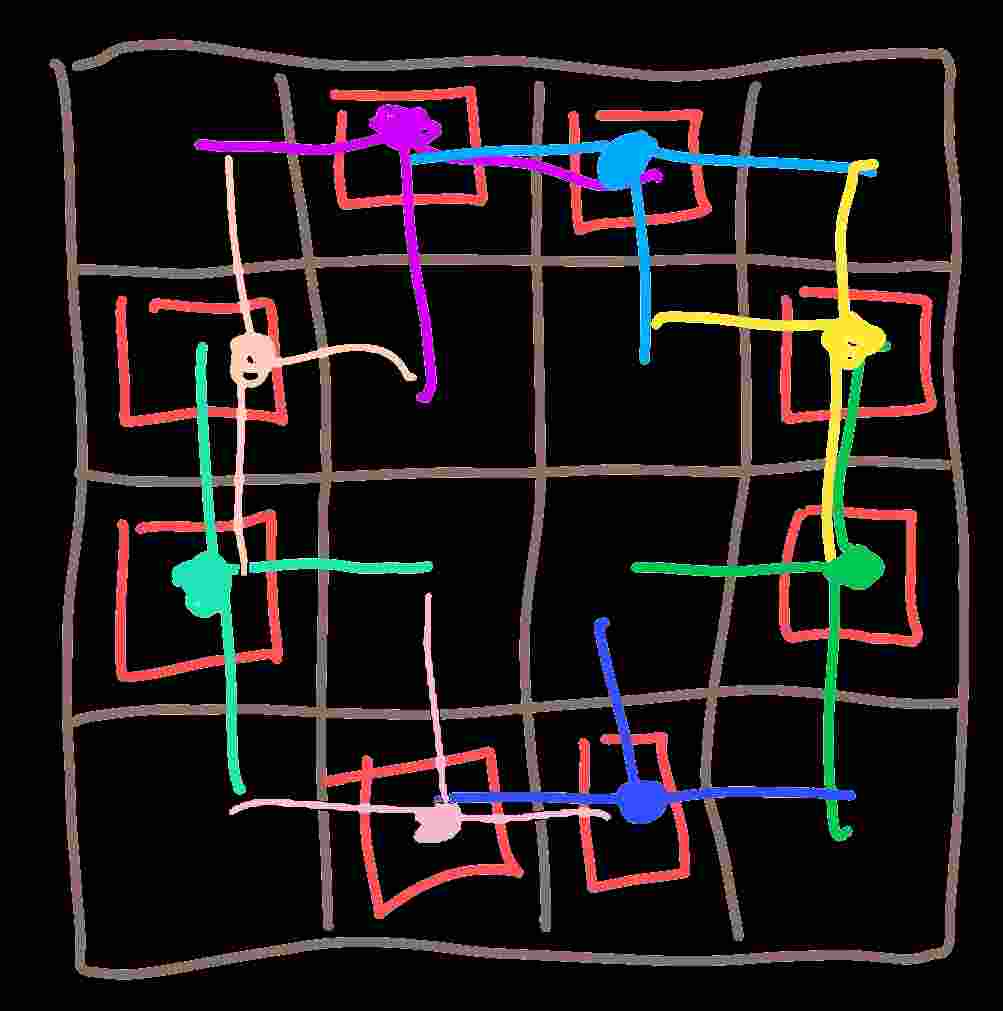
the game takes the current stepstate and xor's it with each equivalency, then replaces the stepstate with the simplest one it found. i assume this is an exhaustive search of possible solutions for a given board. for 3x3, all solutions are unique. for 4x4 there are fifteen of these equivalencies. for 5x5 theres weirdly only 3? because of this i kinda suspect 4x4 is the easiest mode lol
every one of these equivalencies ive generated have an even number of steps to them. this means that an odd stepstate cant be equivalent to an even one and vice versa. additionally, if it took an even number of steps to go from a blank board to the shuffled board, itll take an even number of steps to put it back, no matter the path you take. every new game starts with a blank board and makes as many random moves as there are squares, so every 4x4 game will take an even number of steps to solve, and every 5x5 game will take an odd number.
representational inconsistency
the code for my flip is based on the code for my towers, internally its an array of cells with their own properties like whether its in the stepstate and whether its black or white. the cross shape is flipped because each cell has a list of other cells that flip when it flips. the stepstate is calculated simply by keeping track of what cells have been flipped directly
to precalculate all possible stepstates to generate the list of equivalencies i had to totally remake the logic of the game in a different way. flipping a square from black to white or back is equivalent to xor'ing a bit with one. so the python script centers around a function that takes a number as an input that in binary represents a stepstate, with a one in every place a red square would be in the solver. by bitshifting that number you can move all the ones in a stepstate one space up down left and right. if you take all these copies and xor them together youve gone directly from a stepstate to a boardstate with theoretically super fast operations
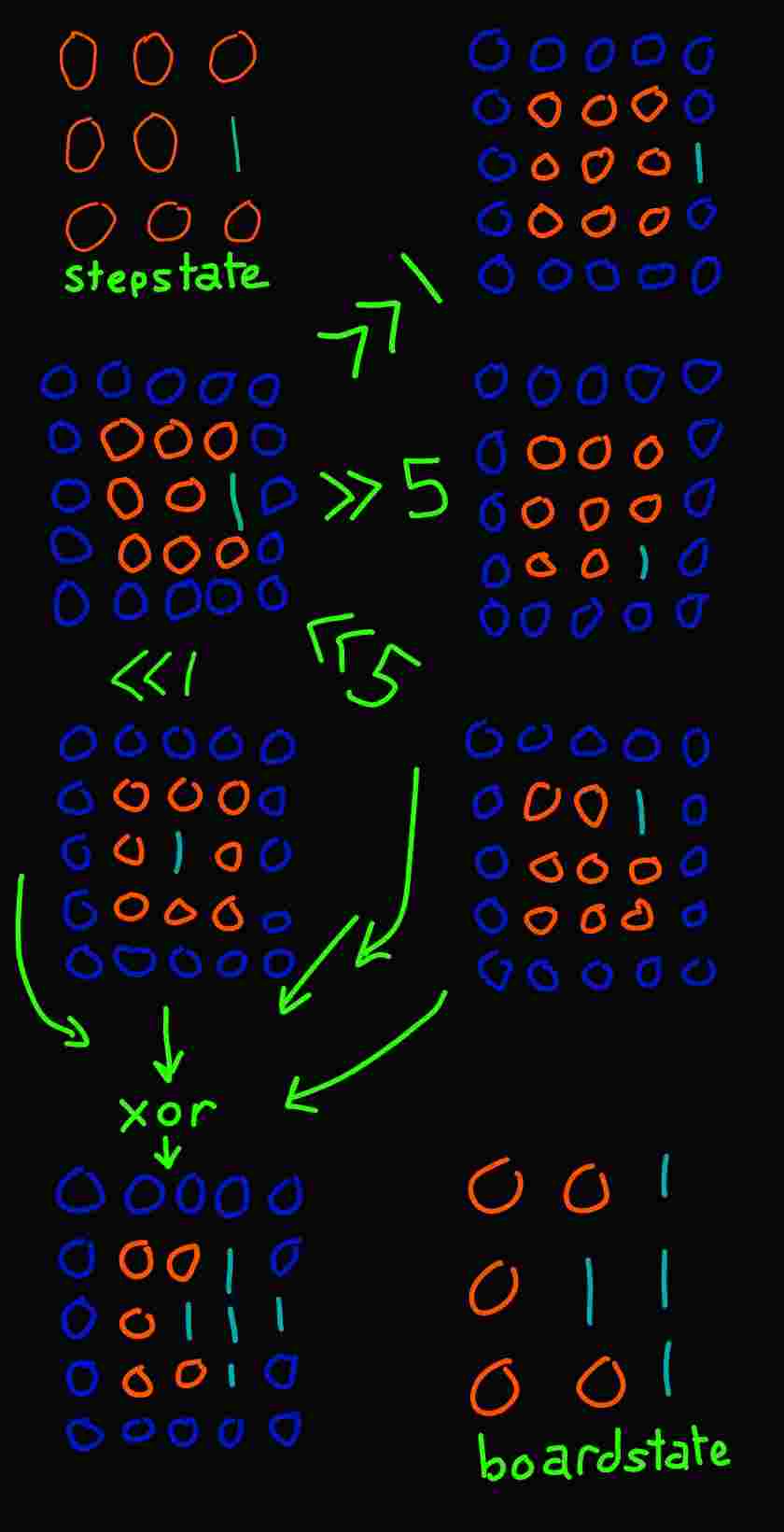
in practice i suspect its slow because of having to cast the number as a string to wrap it in zeros and stuff
O(2^n)
the exhaustive search must calculate the boardstate for every possible stepstate. every square may have either a 0 or a 1 in its stepstate, so there are as many stepstates as there are binary numbers with as many digits as there are squares
| 3x3 | 29 = 512 |
|---|---|
| 4x4 | 216 = 65,536 |
| 5x5 | 225 = 3,355,432 |
| 6x6 | 236 = 68,719,476,736 |
if precalculating the 5x5 equivalencies took my phone 15 minutes, doing the 6x6 equivalencies would take her 21 days